¿Te podemos ayudar?

PROYECTO
Generación de modelo de interpolación de la temperatura promedio en Aragón, España a través del método Kriging
PROYECTO DEL CURSO

Geoestadística aplicada al medio ambiente
REALIZADO POR

Federico Hartmut Garland Schiefer
Introducción
La geoestadística constituye la pluralidad de técnicas utilizadas para estudiar el comportamiento de variables numéricas que se distribuyen espacialmente. Es una herramienta muy útil para explicar la variabilidad de fenómenos en el espacio. Su finalidad principal es la estimación de los valores de una variable en sitios donde esta no ha sido medida, a partir de puntos con valores conocidos, lo que se conoce como interpolación. A través de esta técnica se pueden generar mapas de superficies contiguas a partir de un número reducido de puntos de muestreo. Además, no solo permite estimar los valores sino también calcular el error de la estimación (González et al., 2007).
A través de la geoestadística se pueden generar modelos de interpolación que describan con alta precisión la variabilidad espacial de magnitudes en el espacio, como la temperatura.
Antecedentes
Existen múltiples experiencias del uso de modelos de interpolación geoestadísticos para la estimación de la variabilidad espacial de factores climáticos como la temperatura.
Bustamante (2003) utilizó métodos de interpolación como Kriging y regresión múltiple para generar cartografía predictiva de la temperatura promedio mensual en España peninsular, a partir de los datos de estaciones meteorológicas georreferenciadas, obteniendo un error medio de estimación del 9%.
Asimismo, Varentsov et al. (2019) generó mapas continuos de alta resolución de la temperatura en Noruega a partir de distintos modelos de interpolación Kriging.
Área de Estudio
Aragón es una región y comunidad autónoma de España ubicado en la zona noreste del país. Cuenta con una superficie total de 47 719 km2, de las cual aproximadamente el 48.8% corresponde a tierras de uso agrícola, y 49.7% a espacios forestales o abiertos. Asimismo, presenta valores de altitud que van desde los 65 hasta los 3400 m.s.n.m, con el 40% de los municipios ubicados en zonas de montaña. Además, presenta 7 tipos distintos de clima (Instituto Aragonés de Estadística, 2013).
Dado que la región de Aragón cuenta con vastas zonas destinadas a la producción agrícola y otras actividades económicas, y presenta además una alta diversidad de climas y altitudes, es pertinente conocer la distribución espacial de la temperatura en la región para facilitar la toma de decisiones en actividades que se puedan ver influenciadas por esta variable.
Objetivos
- Determinar la variabilidad espacial de la temperatura promedio en Aragón a través de análisis geoestadístico e interpolación.
- Generar un modelo de interpolación de alta confiabilidad para la temperatura promedio en Aragón.
Metodología
Para la generación del modelo de interpolación y mapa final de temperatura promedio en Aragón se siguió la metodología planteada en el siguiente flujograma.
Figura 1. Flujograma del proceso de generación del modelo geoestadístico de interpolación

- Análisis Exploratorio
En primer lugar, se realizó un análisis exploratorio de los datos para poder describir el comportamiento de la variable en la muestra y posteriormente poder variar los parámetros del modelo de interpolación para ajustarlo a la realidad y disminuir el error.
a. Histograma
Figura 2. Histograma de frecuencias para la temperatura promedio en Aragón

Se observa que el valor de de curtosis de 3.1884 y el de asimetría de -0.81339 y. Esto indica que la distribución de los datos es leptocúrtica y presenta asimetría negativa, por lo que podemos inferir que no sigue una distribución normal.
Para intentar corregir esto se realizó una transformación logarítmica y Box-Cox.
Figura 3. Histograma de frecuencias con transformación logarítmica para la temperatura promedio en Aragón

La transformación logarítmica arrojó valores más pronunciados de curtosis y asimetría, por lo que se descarta el uso de esta.
Figura 4. Histograma de frecuencias con transformación Box-Cox para la temperatura promedio en Aragón

La transformación Box-Cox no modificó los valores de curtosis ni asimetría, por lo que también se descarta su uso.
b. Normal Q-Q Plot
Se analizó el gráfico de Normal Q-Q Plot para evaluar si los datos siguen una distribución normal.
Figura 5. Normal Q-Q Plot para la temperatura promedio en Aragón

Se observa un claro desajuste entre los datos y la curva de distribución normal. Aparentemente, los datos por debajo de 17.5 °C son los que más se alejan de la distribución normal, seguidos por los datos ubicados por encima de 22 °C.
Figura 6. Selección de primer set de datos con mayor alejamiento de la curva normal

Se observa que los valores que más se alejan de la curva normal, son aquellos ubicados en los extremos de las zonas Norte y Sur. Para acercar los datos a la normalidad, podría sugerirse un aumento del número de muestras en estas zonas.
Figura 7. Selección de segundo set de datos con mayor alejamiento de la curva normal

Se observa que en la zona Centro a Centro-Este existen también algunos datos que difieren bastante de la curva normal. Podría también recomendarse un mayor muestreo en esta zona para intentar normalizar los datos.
c. Mapa de Voronoi
Se utilizó un Mapa de Voronoi tipo “Media” para visualmente buscar tendencias en la distribución de los datos.
Figura 8. Mapa de Voronoi tipo “Media” para la temperatura promedio en Aragón

Se observa una aparente tendencia de Norte a Sur, donde los datos en el Norte presentan valores bajos, luego aumentan a valores altos en el Centro, y vuelven a presentar valores bajos en el Sur. A su vez, en la zona central de Aragón se observa cierta tendencia de Este a Oeste, siendo los valores altos en el Este y bajos en el Oeste.
d. Análisis de Tendencias
Se utilizó la herramienta de Análisis de Tendencias para encontrar las tendencias de datos en los ejes X (Este-Oeste) y Y (Norte-Sur), además de poder identificar el Orden de Polinomio que mejor se ajusta a la tendencia de los datos.
Figura 9. Tendencia de la temperatura en eje Y – Sur a Norte

Se observa una tendencia parabólica, donde los valores presentan medidas bajas en el Norte, altas en el Centro y nuevamente bajas en el Sur. Además, el polinomio que presenta mejor ajuste es el de orden 2.
Figura 10. Tendencia de la temperatura en eje X – Este a Oeste

Se observa una ligera tendencia en el eje X, donde los valores son bajos en el Oeste y ligeramente más altos en el Este. El polinomio de mayor ajuste es también de orden 2.
Entre los 2 ejes, los datos parecen mostrar una tendencia más marcada en el eje Y, presentando una curva parabólica negativa.
e. Semivariograma
Se analizó el semivariograma para determinar el grado de autocorrelación espacial existente en los datos.
Figura 11. Semivariograma empírico para la temperatura promedio en Aragón

Se observa que los puntos se concentran a distancias cortas y se dispersan a mayores distancias, lo que confirma la presencia de autocorrelación espacial.
f. Covarianza
Figura 12. Covarianza para la temperatura promedio en Aragón
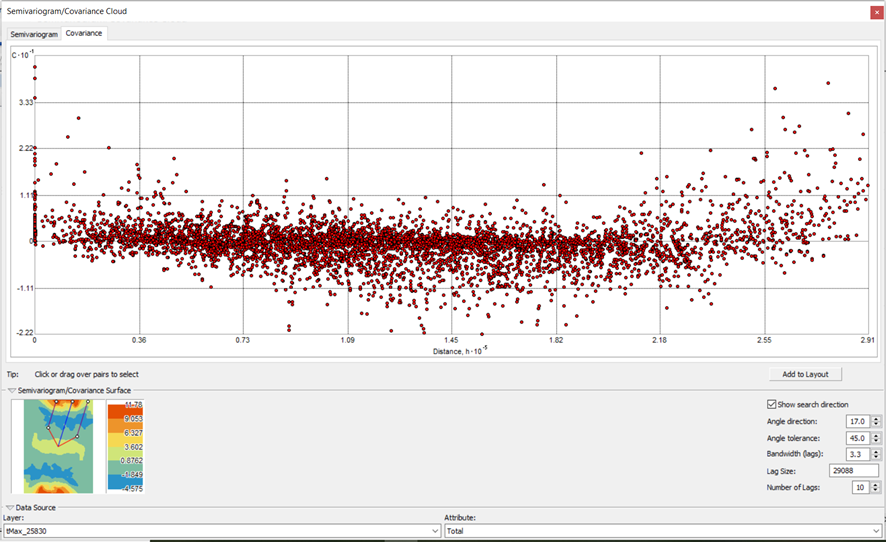
Se observa que la covarianza sigue una tendencia constante.
2. Selección de método de interpolación
Si bien los datos no siguen una distribución normal, existe un buen grado de autocorrelación espacial como se evidencia en el semivariograma, por lo que se utilizó un módelo de interpolación Kriging Ordinario.
3. Muestreo Aleatorio
Se realizaron 4 muestreos aleatorios al 80% del total, a través de la herramienta Subset Features, generando un total de 4 muestras de entrenamiento y 4 muestras de test que serán utilizadas para la validación. Para cada muestra de entrenamiento la muestra es igual a n=106, y para cada muestra de test n=27.




4. Interpolación Kriging
Se realizó una interpolación por Kriging Ordinario al campo “Total”, sin transformación y en Order of Trend Removal de 2. Este proceso se realizó 2 veces por cada muestra de entrenamiento, una vez dejando las opciones por defecto y otra variando los parámetros del método en función al análisis exploratorio. Cada muestra de entrenamiento fue a su vez sometida a un análisis exploratorio particular para ajustar los parámetros adecuadamente.
A continuación se muestra el procedimiento de realización del modelo:



En el semivariograma, se activó la opción de mostrar la dirección de búsqueda y se ajustaron distintos tipos de semivariograma a los puntos. En base a ello, se modificó el tipo de semivariograma a uno Gaussiano. Además, se cambió el número de Lags de 12 a 11.

En las propiedades de búsqueda de vecinos, se modificó el ángulo a 10 grados. Además, se aumentó el tamaño del Major semiaxis de 68 000 a 100 000, y se disminuyó el Minor semiaxis de 68 000 a 50 000. Esto se realizó para que el vecindario de búsqueda abarque una mayor superficie de Norte a Sur y pueda captar la tendencia que habíamos encontrado en esta orientación durante el análisis exploratorio.

Aquí se pudieron observar los valores de error de la validación cruzada del modelo, comprobándose que se acerquen a 0.
Figura 13. Modelo de interpolación Kriging de temperatura promedio para la muestra entrenamiento 1

Al comparar los valores de validación cruzada entre el modelo por defecto y el de parámetros modificados, se constató que el modelo con los parámetros modificados presenta menor Error Medio y Root-Mean-Square que el modelo con los parámetros por defecto. El modelo modificado presenta un error medio de 0.0082 mientras que el modelo por defecto presenta un valor de 0.0299. De igual manera, el modelo modificado presenta un Root Mean Square de 1.146 mientras que el modelo por defecto presenta un valor de 1.172.
Figura 14. Comparación de medidas de validación cruzada entre el modelo con variación de parámetros y el modelo por defecto.

Este mismo procedimiento se realizó para las 4 muestras de entrenamiento.
5. Recorte de Modelos
Para recortar el modelo escogido, primero se exportó la capa a formato Raster y luego se utilizó la herramienta “Extract by Mask” delimitando como capa de contención a los límites territoriales de Aragón.
Finalmente, se modificó la simbología para generar las clases correspondientes.
A continuación, se muestran los 4 modelos de interpolación obtenidos, uno para cada muestra de entrenamiento.




6. Validación
Una vez obtenidos los modelos de cada una de las 4 muestras de entrenamiento, se realizó la validación de cada uno de ellos a través de la muestra Test correspondiente.
Para ello, se utilizó la herramienta de Validation/Prediction. Una vez obtenida la capa de validación se añadió un campo adicional (llamado “RMS”) que corresponde a los valores del Error Cuadrado para poder calcular el Root Mean Square, que seria equivalente a la raíz cuadrada de la media del error cuadrado. Asimismo, se desplegaron las estadísticas del campo Error para observar el Error Medio de la validación.

De esta forma se consiguieron los errores medios de la validación de los 4 modelos.
7. Comparación de modelos y selección de modelo final
La comparación de modelos se hizo cotejando los valores del Error medio del modelo (el que figura en la validación cruzada al final del método de interpolación), y el Error medio de validación (el calculado con la muestra test).
Figura 15. Comparación de validación cruzada de los 4 modelos de interpolación


Figura 16. Comparación de valores de validación test para los 4 modelos de interpolación




Finalmente, se resumieron los valores de error en una tabla de comparación.
Tabla 1. Comparación final de medidas de error entre los 4 modelos de interpolación
| Modelo | Error medio modelo | Error medio validación |
| 1 | 0.008216 | -0.10354 |
| 2 | -0.002769 | 0.040129 |
| 3 | 0.024121 | 0.10729 |
| 4 | 0.0286221 | -0.237331 |
En base a estos valores se realizó la selección del modelo final de interpolación. Se obtuvieron los menores valores de Error medio y Error medio de validación con el modelo número 2, por lo que este será utilizado en el mapa final.
Resultados
Se obtuvo un mapa final de la temperatura promedio en Aragón, utilizando los resultados del Modelo 2 y añadiendo a la presentación gráficos del análisis exploratorio, las medidas de error del modelo, el gráfico de ajuste de predicción de la validación cruzada, y otros elementos adicionales.
Figura 17. Mapa Final de Modelo de Interpolación de Temperatura Promedio en Aragón

Se observa un alto grado de variabilidad espacial de la temperatura promedio en la región de Aragón. Los valores de temperatura son bajos en el Norte y en el Sur, y altos en la zona Centro. Esto coincide con la distribución de la elevación en la región de Aragón, existiendo una relación proporcional inversa entre la elevación y la temperatura. Las medidas de error medio del modelo son bastante cercanas a 0, y la raíz del error medio cuadrático es cercano a 1, por lo que se puede afirmar que el modelo presenta un buen nivel de precisión.
Conclusiones
- La temperatura promedio en Aragón presenta un alto grado de variabilidad espacial.
- Existe una relación proporcional inversa entre la elevación y la temperatura promedio en la región.
Recomendaciones
- Se recomienda a los agentes económicos en Aragón tener en consideración la variabilidad espacial de la temperatura al momento de tomar decisiones referentes a la ubicación de sus actividades.
- Es recomendable establecer en cada zona de temperatura cultivos agrícolas que se adecuen al contexto climatológico, para maximizar los rendimientos y disminuir las complicaciones.
Referencias
Instituto Aragonés de Estadística. (2013). Datos Básicos de Aragón. http://www.observatoriohuesca.com/fotosbd/160920131437331082.pdf
Bustamante, J. (2003). CARTOGRAFÍA PREDICTIVA DE VARIABLES CLIMÁTICAS: COMPARACIÓN DE DISTINTOS MODELOS DE INTERPOLACIÓN DE LA TEMPERATURA EN ESPAÑA PENINSULAR. https://digital.csic.es/bitstream/10261/47147/1/252-282-1-PB.pdf
Varentsov, M., Esau, I., Wolf, T. (2019). High-Resolution Temperature Mapping by Geostatistical Kriging with External Drift from Large-Eddy Simulations. https://www.researchgate.net/publication/337850623_High-Resolution_Temperature_Mapping_by_Geostatistical_Kriging_with_External_Drift_from_Large-Eddy_Simulations
González, J., Guerra, F., Gómez, H. (2007). CONCEPTOS BÁSICOS DE GEOESTADÍSTICA EN GEOGRAFÍA Y CIENCIAS DE LA TIERRA: MANEJO Y APLICACIÓN. https://www.redalyc.org/pdf/360/36014577008.pdf
REALIZADO POR

Federico Hartmut Garland Schiefer
PROYECTO DEL CURSO

Geoestadística aplicada al medio ambiente
Alejandra Duque